ではどういう数学教育が良いのか?
私の娘が高校で「数学は勉強しなくてもわかる」というレベルに達したのには、3つの理由があると私は信じている。
ひとつは、幼いときに高速計算練習をしなかったことである。もうひとつは、そういう同級生(と彼らの母親たち)に馬鹿にされて「私は数学ができない」と悲観している彼女に、「早く計算できることと数学ができることは同じではない。後にそれを証明してみせるから、お母さんを信じなさい」と自信を持って約束し続けたこと。そして最後に、中学校で理想的な数学教師を獲得したことである。
娘が通った中学校では、子供の学習スタイルに会った教育チームを希望することができる。私が唯一希望したのは、ロシア出身の数学教師タチアナ・フィンケルスタインである。
変人として有名な彼女は保護者への説明会で一方的にこう語る。
「いつも尋ねられることですが、私は教科書は使いません。なぜかというと、教科書はBadだからです。私は使いませんが教科書は渡します。見たい人は勝手に見てもらってけっこうです。役には立たないと思いますけれどね。いろんなことを子どもに詰め込んで、そのときだけできても意味はありません。子どもたちはよく、『あ、それ知ってる、知ってる』と言います。すると私は、『じゃ、説明して』と要求します。そうしたら子どもたちは、『見たことはあるけれど、忘れた』と言います。一回習っても、それは『聞いたことがある』とか『見たことがある』程度なんです。知ってることにはならない」
彼女は「教科書を使わない」という発言に表情を曇らせる親を見てもひるまない。
「教科書がないのにちゃんとカリキュラムを終えられるのかどうか心配する親がいますけれど、大丈夫です。教科書なんかなくても、生徒はちゃんと必要なことは全部学びます」
授業もそんな感じである。
「もし猫を見たら、あなたたちは猫だとわかるかね?」
いきなりそんなことをたずねる。
生徒たちは、裏がありそうだと思いつつもいっせいに答える。
「もちろんわかるよ」、「見たらわかるに決まってんじゃない」
思惑通りの答えにフィンケルスタインはにやりと笑う。
「でも、なぜ猫だとわかる?」
犬にも尖った耳や長いしっぽがあるものもあるし、ネズミにもヒゲがある。猫とはどういう動物のことを言うのか。目の前の動物がそうだと断定するためには、どんな証拠が必要なのか。
しんとした生徒たちを見渡して、フィンケルスタインはロシア語なまりの強い英語で諭す。
「他人が『あれは猫だ』と言っても、そのまま信じちゃいかんよ」
こうして「定義と証明」について学んだ生徒がそれを忘れそうになったころ、フィンケルスタインは生徒にまたこんな質問をする。
「無理数って知ってるかね?」
「円周率は無理数だよ」
「円周率が無理数だってなんでわかるの?」
フィンケルスタインは口数が少なくなった生徒に繰り返す。
「他人が『あれは猫だ』とか『円周率は無理数だ』と言ってもそのまま信じちゃいかん。人は知らなくても知ったフリをするもんなんだから。信用できるのは自分だけなんだよ。自分でそれを証明するまでは、猫に見えても猫じゃないと思わなくちゃ」
全国的に有名なレキシントン高校の数学チームでキャプテンを務めるジュリア・ジェングは、両親がそろってアイビーリーグの大学院を卒業した中国人だが、(アジア系移民としては)ユニークな教育方針のために幼いときに高速計算練習をさせられていない。だから、私の娘のように小学校時代は算数が嫌いで「私は数学ができない」と信じていた。空想好きで小学生のときからファンタジー小説を書いて友達に読ませていたジュリアの得意科目は国語だった。
そんな彼女を数学好きにしたのは、フィンケルスタインが新入生に勧めるミヒャエル・エンデの「果てしない物語」とアントワーヌ・ド・サン=テグジュペリの「星の王子様」だった。フィンケルスタインの言葉に耳を傾けているうち、ファンタジーと数学の世界には共通点があると思うようになった。ひとつの謎を解くたびに、物語の真相に近づいてゆくのがゾクゾクするほど面白い。謎を解く鍵である数学理論をもっと知りたいと思ったのが数学好きになるきっかけだった。
これは、フィンケルスタインが新6年生(レキシントンでは中学校1年生)の最初の週に与える宿題のひとつである。
--------
ほんの少し昔のこと。怠け者イワンがロシアの橋の妖精トロールに会いに行った。そのときの話を聞かせてあげよう。
怠け者イワンは独り言を言った。
「みんな仕事を見つけるか、さもなくはトロールと取引しろと言うけれども、トロールが僕を金持ちにしてくれるなんて思えないなぁ」
そう言い終えるやいなや、近くの橋からトロールが現れてこう尋ねた。
「イワン、おまえは金持ちになりたいんだね」
イワンはうなずいた。
「じゃあ、おまえが橋を渡るたびにポケットの中にある金を倍にしてやろう。おまえは、橋を渡るだけでいい」
早速橋を渡り始めたイワンをトロールが呼び止めた。
「こんなに気前よくしてやっているのだから、私の苦労にちょっとした礼をくれてもいいんじゃないか?どうだい、橋を渡るたびに8ルーブルくれるってのは」
イワンはトロールの申し出を承諾し、いそいで橋を渡った。ポケットに手を入れると、魔法のようにお金は倍になっているではないか。そこでイワンはトロールに8ルーブル投げ渡した。2回めも3回めもポケットの中の金は倍になったが、3回目に8ルーブルを渡したところ、ポケットの中は空になっていた。
トロールは大笑いをして姿を消した。
さて、タチアナも自分の運を試してみようと思った。
しかし、3回橋を渡り終えたところで、彼女はトロールにこう叫んだ。
「なんてことよ!ミスター・トロール、私の手持ちのお金はあなたに会う前とまったく同じじゃないの。前よりも金持ちでもなければ、貧乏でもない。とんでもない橋の魔法だわ」
タチアナとイワンが最初に持っていたお金はいくらだったのかな?
(答えはこちら。でも次の問題もあるので、後回しにすることをおすすめ)
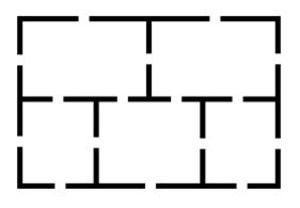
次もフィンケルスタインが6年生に出す「五つの部屋がある家」(下記の図)の問題だ。
「すべてのドアを一度だけ通るとして、全部のドアを通ることは可能か?」という難問である。
フィンケルスタインは簡単に答えを与えず何週間も悩ませておく。思考する過程こそが重要だと思っているからだ。だから時間ができると生徒は自主的に黒板に集まってああでもない、こうでもないと言い合う。
「この問題は、outside box(箱の外、つまり既定の思考の枠組の外で考える。独創的という意味)でないとダメだ……」独り言を大声でつぶやきながら、黒板に箱の絵を描いている子もいる。
一日じっくりひとつの教科を学ぶ「プロジェクトデー」でオイラー閉路やハミルトン閉路を試みるのも同様の理由だ。これらは、「一筆書き」のようにそれぞれグラフのすべての辺、あるいは点を一度だけ通る閉路のことで、大学のグラフ理論で研究されたりする難問だ。
実は、先の「五つの部屋がある家」もこの種の質問である。「できるかできないか?」、「それはなぜなのか?」、「そこにパターンはあるのか?」と自由に話し合うことで、生徒たちは、「自分の頭を使う」訓練をするのである。
(答えはこちら)
教科書を使わないので親も子も気づかないが、ノートや宿題を見ると、6年生の9月から5月までのたった9ヶ月で素因数分解や連立方程式、不等式だけでなく、円の性質や確率、平方根、ピタゴラスの定理と証明、相似図形など日本の中学3年間で教わることをほとんど学んでいる。
私の娘は中学の推薦で13歳のときに大学入学選考に使われる共通試験のSATを受け、数学で4問ケアレスミスをしただけで残りは全問正解だった。試験のための勉強はまったくしていない。すべて学校で学んだ知識だけで十分答えられる内容だったという。
教科書を使い、放課後に塾に通う生徒たちよりもフィンケルスタインの生徒が数学ができるようになるのは、生徒に自分の頭を使って謎を解くことの喜びを教えるからである。
フィンケルスタインを取材したときに、最も心に残ったのが次の言葉である。幼い子供を育てている親にはぜひ読んでもらいたい。
親や教師の言動で最悪なのは、「今おまえがやっていることはすべて、将来のためなのだ」と教えること。まるで今よりも将来のほうが良いことがあるみたいにね。でも、そういう人は「今を楽しまずに嫌いなことを一生懸命やるのは将来のためだ」という態度を大人になってもずっと続けてるでしょ。まるで、それを続けていると死を免れるかのように。でもね、誰だって最後には死ぬんだから。
そういうことを言う大人が今楽しそうに生きていなかったら、子どもは「何のために今がまんしなければならないんだろう?」と思うでしょ。
子ども時代ってのは、一番楽しいものなんですよ。だから、楽しませなくちゃ。大人になるために子供時代を犠牲にするのはもったいない。