怠け者イワンとトロールの物語
タチアナ8ルーブル、イワン7ルーブル。
正しい解き方というのはない。一番手っ取り早いのは、物語を2{2(2x-8)-8}-8=0という式にすることだが、小学校5年生が終わった時点ではまだ代数学を学んでいない。
日本で教育を受けた者には、方程式で素早く簡潔に解くのが良いことだ、という固定観念がある。ところが、フィンケルスタインは、この時点ではまだ習っていない代数学を使って解いた子よりも、独自の方法で解答にたどり着いた子を褒める。コンセプトを理解せずに正解を得たところで、それが親か公文塾から習った付け刃だということを彼女は察しているのだろう。
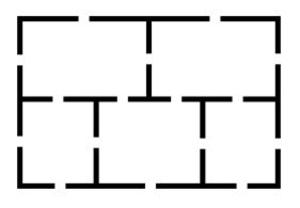
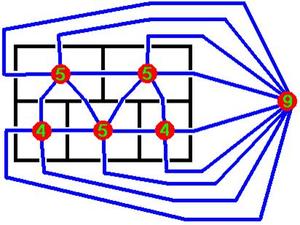
「五つの部屋がある家のパズル」の答え
答えは、「不可能」。
18世紀の数学者レオンハルト・オイラーの有名な「ケーニヒスベルクの橋の問題」に類似したもの。オイラーは、橋の問題で一筆書きが可能になる必要十分条件を見つけた。頂点から出る枝が奇数のものがゼロか二つの場合にのみ可能になる。五つの部屋の場合、奇数の枝が出る頂点は4つあるので一筆書きは不可能。